A tour of mrcal: differencing

We just gathered calibration images and computed some calibrations.

An overview follows; see the differencing page for details.

We just used the same chessboard observations to compute the intrinsics of a lens in two different ways:

• Using a lean LENSMODEL_OPENCV8 lens model
• Using a rich splined-stereographic lens model

And we saw evidence that the splined model does a better job of representing reality. Can we quantify that?

Let's compute the difference. There's an obvious algorithm: given a pixel \(\vec q_0\) we

1. Unproject \(\vec q_0\) to a fixed point \(\vec p\) using lens 0
2. Project \(\vec p\) back to pixel coords \(\vec q_1\) using lens 1
3. Report the reprojection difference \(\vec q_1 - \vec q_0\)

This is a very common thing to want to do, so mrcal provides a tool to do it. Let's compare the two models:

mrcal-show-projection-diff \
  --intrinsics-only        \
  --cbmax 15               \
  --unset key              \
  opencv8.cameramodel      \
  splined.cameramodel

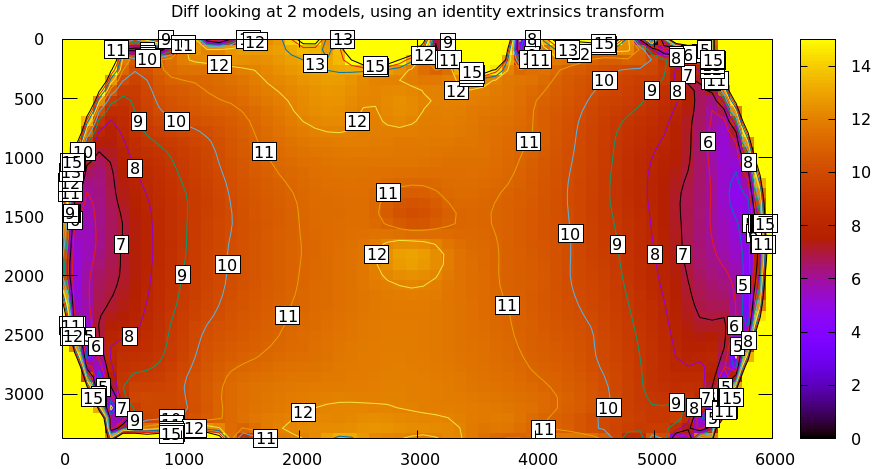
Well that's strange. The reported differences really do have units of pixels. Are the two models really that different? If we ask for the vector field of differences instead of a heat map, we get a hint about what's going on:

mrcal-show-projection-diff \
  --intrinsics-only        \
  --vectorfield            \
  --vectorscale 10          \
  --gridn 30 20            \
  --cbmax 15               \
  --unset key              \
  opencv8.cameramodel      \
  splined.cameramodel

This is a very regular pattern. What does it mean?

The issue is that each calibration produces noisy estimates of all the intrinsics and all the coordinate transformations:

The above plots projected the same \(\vec p\) in the camera coordinate system, but that coordinate system has shifted between the two models we're comparing. So in the fixed coordinate system attached to the camera housing, we weren't in fact projecting the same point.

There exists some transformation between the camera coordinate system from the solution and the coordinate system defined by the physical camera housing. It is important to note that this implied transformation is built-in to the intrinsics. Even if we're not explicitly optimizing the camera pose, this implied transformation is still something that exists and moves around in response to noise. Rich models like the splined stereographic models are able to encode a wide range of implied transformations, but even the simplest models have some transform that must be compensated for.

The above vector field suggests that we need to pitch one of the cameras. We can automate this by adding a critical missing step to the procedure above between steps 1 and 2:

• Transform \(\vec p\) from the coordinate system of one camera to the coordinate system of the other camera

We don't know anything about the physical coordinate system of either camera, so we do the best we can: we compute a fit. The "right" transformation will transform \(\vec p\) in such a way that the reported mismatches in \(\vec q\) will be small. Lots of details are glossed-over here. Previously we passed --intrinsics-only to bypass this fit. Let's omit that option to get the the diff that we expect:

mrcal-show-projection-diff \
  --unset key              \
  opencv8.cameramodel      \
  splined.cameramodel

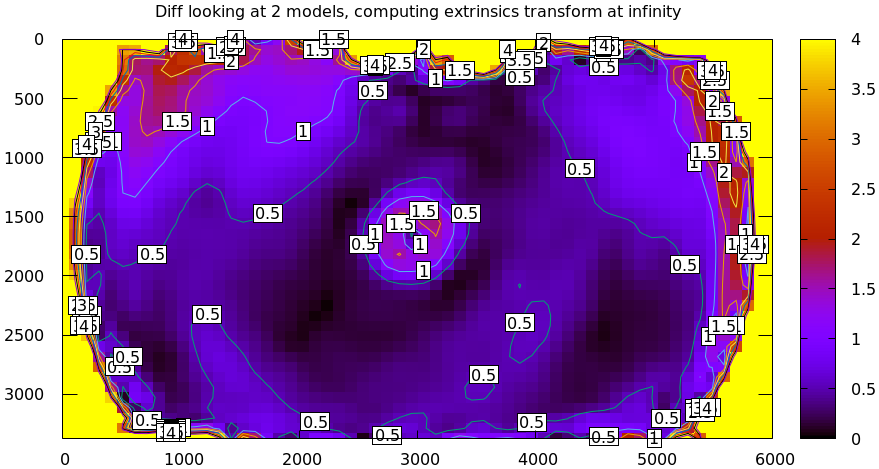
Much better. As observed earlier, the Sony Alpha 7 III camera is applying some extra image processing that's not modeled by LENSMODEL_OPENV8, so we see an anomaly in the center. The models agree decently well past that, and then the error grows quickly as we move towards the edges.

This differencing method is very powerful, and has numerous applications. For instance:

• evaluating the manufacturing variation of different lenses
• quantifying intrinsics drift due to mechanical or thermal stresses
• testing different solution methods
• underlying a cross-validation scheme to gauge the reliability of a calibration result

Many of these analyses immediately raise a question: how much of a difference do I expect to get from random noise, and how much is attributable to whatever I'm trying to measure?

These questions can be answered conclusively by quantifying a model's projection uncertainty, so let's talk about that now.

Now we compute the projection uncertainties of the models