mrcal splined lens models

The LENSMODEL_SPLINED_STEREOGRAPHIC_... model is a stereographic model with correction factors. To compute a projection using this model, we first compute the normalized stereographic projection \(\vec u\) as in the LENSMODEL_STEREOGRAPHIC definition:

\[ \theta \equiv \tan^{-1} \frac{\left| \vec p_{xy} \right|}{p_z} \]

\[ \vec u \equiv \frac{\vec p_{xy}}{\left| \vec p_{xy} \right|} 2 \tan\frac{\theta}{2} \]

Then we use \(\vec u\) to look-up a \(\Delta \vec u\) using two separate splined surfaces:

\[ \Delta \vec u \equiv \left[ \begin{aligned} \Delta u_x \left( \vec u \right) \\ \Delta u_y \left( \vec u \right) \end{aligned} \right] \]

and we then define the rest of the projection function:

\[\vec q = \left[ \begin{aligned} f_x \left( u_x + \Delta u_x \right) + c_x \\ f_y \left( u_y + \Delta u_y \right) + c_y \end{aligned} \right] \]

The \(\Delta \vec u\) are the off-stereographic terms: if \(\Delta \vec u = 0\), we get a plain stereographic projection.

The surfaces \(\Delta u_x\) and \(\Delta u_y\) are defined as B-splines, parametrized by the values of the "knots" (control points). These knots are arranged in a fixed grid in the space of \(\vec u\), with the grid density and extents set by the model configuration (i.e. not subject to optimization). The values at each knot are set in the intrinsics vector, and this controls the projection function.

We're using B-splines primarily for their local support properties: moving a knot only affects the surface in the immediate neighborhood of that knot. This makes our jacobian sparse, which is critical for rapid convergence of the optimization problem. Conversely, at any \(\vec u\), the sampled value of the spline depends only on the knots in the immediate neighborhood of \(\vec u\). A script used in the development of the splined model shows this effect:

We sampled a curve defined by two sets of cubic B-spline control points: they're the same except the one point in the center differs. We can see that the two spline-interpolated functions produce a different value only in the vicinity of the tweaked control point. And we can clearly see the radius of the effect: the sampled value of a cubic B-spline depends on the two control points on either side of the query point. A quadratic B-spline has a narrower effect: the sampled value depends on the nearest control point, and one neighboring control point on either side.

This plot shows a 1-dimension splined curve, but we have splined surfaces. To sample a spline surface:

1. Arrange the control points in a grid
2. Sample each row independently as a separate 1-dimensional B-spline
3. Use these row samples as control points to sample the resulting column

Processing columns first and then rows produces the same result. The same dev script from above checks this.

The configuration selects the LENSMODEL_SPLINED_STEREOGRAPHIC_... model parameters that aren't subject to optimization. These define the high-level behavior of the spline. We have:

• order: the degree of each 1D polynomial. This is either 2 (quadratic splines, C1 continuous) or 3 (cubic splines, C2 continuous). At this time, 3 (cubic splines) is recommended. I haven't yet done a thorough study on this, but empirical results tell me that quadratic splines are noticeably less flexible, and require a denser spline to fit as well as a comparable cubic spline.
• Nx and Ny: The spline density. We have a Nx by Ny grid of evenly-spaced control points. The ratio of this spline grid should be selected to match the aspect ratio of the imager. Inside each spline patch we effectively have a lean parametric model. Choosing a too-sparse spline spacing will result in larger patches, which aren't able to fit real-world lenses. Choosing a denser spacing results in more parameters and a more flexible model at the cost of needing more data and slower computations. No data-driven method of choosing Nx or Ny is available at this time, but Nx=30_Ny=20 appears to work well for some very wide lenses I tested with; this is probably overkill. An initial study of the effects of different spacings appears below.
• fov_x_deg: The horizontal field of view, in degrees. Selects the region in the space of \(\vec u\) where the spline is well-defined. fov_y_deg is not included in the configuration: it is assumed proportional with Ny and Nx. fov_x_deg is used to compute a knots_per_u quantity, and this is applied in both the horizontal and vertical directions.

The few knots around any given \(\vec u\) define the value of the spline function there. These knots define "spline patch", a polynomial surface that fully represents the spline function in the neighborhood of \(\vec u\). As the sample point \(\vec u\) moves around, different spline patches, selected by a different set of knots are selected. With cubic splines, each spline patch is defined by the local 4x4 grid of knots (16 knots total). With quadratic splines, each spline is defined by a 3x3 grid.

Since the knots are defined on a fixed grid, it is possible to try to sample the spline beyond the region where the knots are defined (beyond our declared field of view). In this case we use the nearest spline patch, which could sit far away from \(\vec u\). So here we still use a 4x4 grid of knots to define the spline patch, but \(\vec u\) no longer sits in the middle of these knots: because we're past the edge, and the preferred knots aren't available.

This produces continuous projections everywhere, at the cost of reduced function flexibility at the edges: the effective edge patches could be much larger that the internal patches. We can control this by selecting a wide-enough fov_x_deg to cover the full field-of-view of the camera. We then wouldn't be querying the spline beyond the knots, since those regions in space are out-of-view of the lens. fov_x_deg should be large enough to cover the field of view, but not so wide to waste knots representing invisible space. It is recommended to estimate this from the datasheet of the lens, and then to run a test calibration. Running the mrcal-show-splined-model-correction tool then compares the valid-intrinsics region (area with sufficient calibration data) against the bounds of the spline-in-bounds region, letting the user know if the field-of-view is too small.

This splined model has many more parameters, and is far more flexible than the lean parametric models (all the other currently-supported lens models). This has several significant effects.

These models are much more capable of representing the behavior of real-world lenses than the lean models: at a certain level of precision the parametric models are always wrong. The tour of mrcal shows a real-world fit using LENSMODEL_OPENCV8 and a real-world fit using LENSMODEL_SPLINED_STEREOGRAPHIC_..., where we can clearly see that the splined model fits the data better.

The higher parameter counts do result in higher reported uncertainties (see the tour of mrcal for examples). This is a good thing: the lean models report uncertainty estimates that are low, but do not match reality. While the higher uncertainty estimates from the splined models are truthful. This is because the uncertainty estimate algorithm constrains the lenses to the space that's representable by a given lens model, which is a constraint that only exists on paper. Since mrcal reports the covariance matrix of any projection operation, the uncertainty can be used to pass/fail a calibration or the covariance can be propagated to whatever is using the model.

It is thus recommended to use splined models even for long lenses, which do fit the pinhole model more or less.

In the the tour of mrcal we evaluated the projection uncertainty of a splined-model solve:

mrcal-show-projection-uncertainty splined.cameramodel --cbmax 1 --unset key

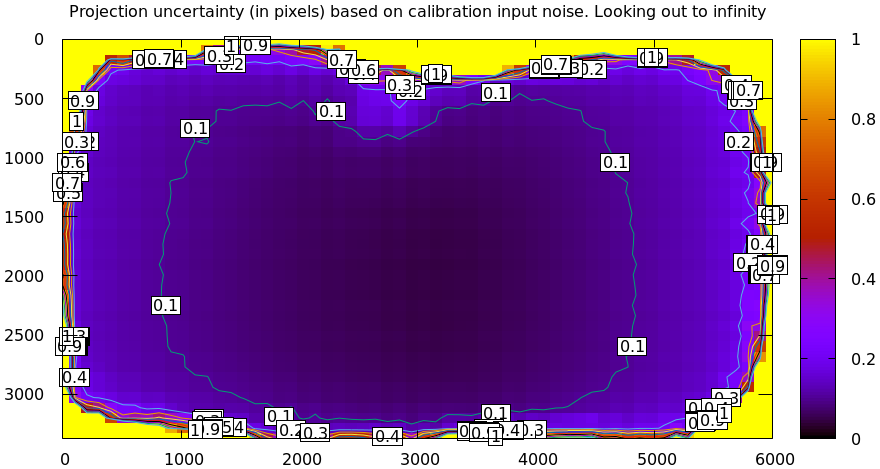
Note that the uncertainties from the splined model don't look smooth. Let's look into that now by evaluating the uncertainty across the imager at \(y = \frac{\mathrm{height}}{2}\). To do this we need to write a bit of Python code:

#!/usr/bin/python3
import mrcal
import numpy as np
import numpysane as nps
import gnuplotlib as gp
from scipy.signal import argrelextrema

m = mrcal.cameramodel('splined.cameramodel')
W,H = m.imagersize()

x = np.linspace(0, W-1, 1000)
q = np.ascontiguousarray( \
      nps.transpose(      \
        nps.cat(x, H/2*np.ones(x.shape))))

v = mrcal.unproject(q, *m.intrinsics())

s = mrcal.projection_uncertainty(v, m,
                                 atinfinity = True,
                                 what = 'worstdirection-stdev')
print(repr(x[argrelextrema(s,np.greater)]))

gp.plot(x, s,
        _with  = 'lines',
        xrange = (0,W-1),
        yrange = (0,0.2),
        xlabel = 'x pixel',
        ylabel = 'Projection uncertainty (pixels)',
        title  = 'Projection uncertainty at infinity, across the image at y=height/2')

We can clearly see the non-monotonicity. This feels like it has something to do with our spline knot layout, so let's check that. The above script also reports the \(x\) coordinates of the local maxima of the uncertainties:

array([  96.08008008,  378.31531532,  558.46546547, 2089.74174174,
       2347.95695696, 2582.15215215, 2828.35735736, 3068.55755756,
       3326.77277277, 3590.99299299, 5716.76476476, 5860.88488488])

Let's look at the knot layout arbitrarily in the region near the center, marking the uncertainty maxima with red lines:

mrcal-show-splined-model-correction                                           \
  --imager-domain                                                             \
  --set 'xrange [2500:3400]'                                                  \
  --set "yrange [$((3376/2+500 )):$((3376/2-500 ))]"                          \
  --set 'arrow from 2582.2, graph 0 to 2582.2, graph 1 nohead lc "red" front' \
  --set 'arrow from 2828.4, graph 0 to 2828.4, graph 1 nohead lc "red" front' \
  --set 'arrow from 3068.6, graph 0 to 3068.6, graph 1 nohead lc "red" front' \
  --set 'arrow from 3326.8, graph 0 to 3326.8, graph 1 nohead lc "red" front' \
  --unset key                                                                 \
  splined.cameramodel

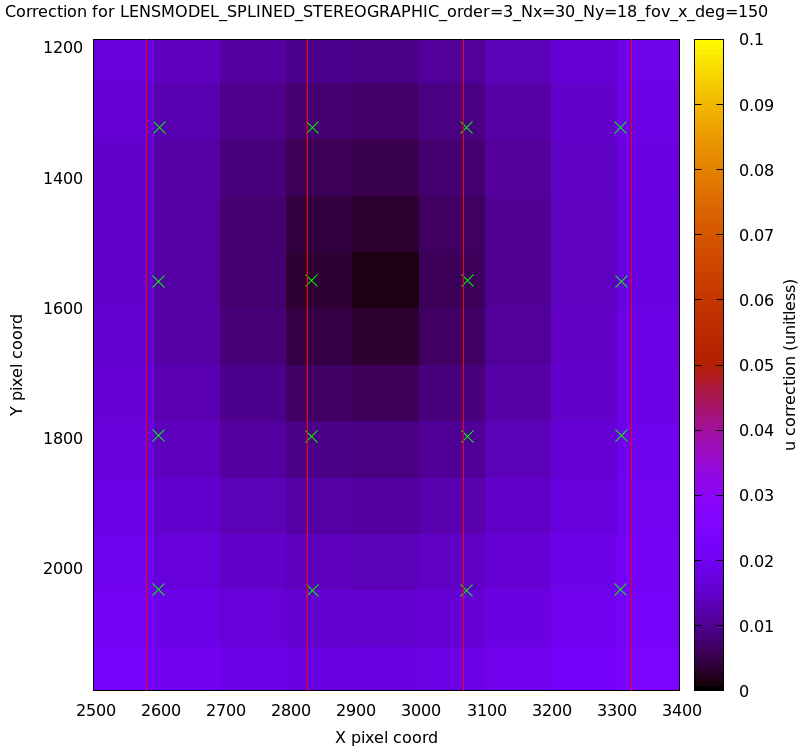
The uncertainty is highest near the knots, so adjusting the spline spacing would have an effect here. I haven't yet studied the effect of changing the spline spacing, but we can do a quick study here. Let's re-run the splined model optimization in the the tour of mrcal, but using different spline spacings. And let's then reconstruct the uncertainty-across-center plot from above for each spacing.

We re-run the solves using this zsh script:

for Ny (4 6 8 10 15 20 25 30) {
  Nx=$((Ny*3/2))

  mrcal-calibrate-cameras                                                               \
    --corners-cache corners.vnl                                                         \
    --lensmodel LENSMODEL_SPLINED_STEREOGRAPHIC_order=3_Nx=${Nx}_Ny=${Ny}_fov_x_deg=150 \
    --focal 1900                                                                        \
    --object-spacing 58.8e-3                                                            \
    --object-width-n 14                                                                 \
    --imagersize 6000 3376                                                              \
    '*.JPG'
}

Results available here. And we write a bit of Python to make our plots:

#!/usr/bin/python3

import mrcal
import numpy as np
import numpysane as nps
import gnuplotlib as gp
import glob
import re

model_paths = np.array(glob.glob(f'splined-Nx=*.cameramodel'))

Nx = np.array([int(re.sub('.*Nx=([0-9]+).*?$', '\\1', p)) \
               for p in model_paths])
i = Nx.argsort()
model_paths = model_paths[i]

models = [mrcal.cameramodel(str(m)) for m in \
          model_paths]

W,H = models[0].imagersize()

x = np.linspace(0, W-1, 1000)
q = np.ascontiguousarray( \
      nps.transpose(      \
        nps.cat(x, H/2*np.ones(x.shape))))

s = np.array([mrcal.projection_uncertainty(mrcal.unproject(q, *m.intrinsics()),
                                           m,
                                           atinfinity = True,
                                           what = 'worstdirection-stdev') \
              for m in models])

legend = np.array([ re.sub('.*(Nx=[0-9]+)-(Ny=[0-9]+).*?$', '\\1 \\2', m) \
                    for m in model_paths ])

gp.plot(x, s,
        _with  = 'lines',
        legend = legend,
        xrange = (0,W-1),
        yrange = (0,0.2),
        xlabel = 'x pixel',
        ylabel = 'Projection uncertainty (pixels)',
        title  = 'Projection uncertainty at infinity, across the image at y=height/2',
        _set   = 'key bottom right',
        wait   = True)

So we can see that as we pick a denser spline:

• The uncertainty increases across the board. We already saw and noted this previously: lean models under-report the uncertainty
• The frequency of the uncertainty wiggle increases. This makes sense: we just noted that the wiggles follow the spline knots.
• The amplitude of the wiggle increases also. This is interesting. It could be due to the fact that a richer spline is better able to squeeze between the gaps between the observed points. Or it could be because dense splines imply smaller spline patches, which means fewer observations are available in any given patch. Or it could be some fundamental property of B-spline-based optimization. This needs a deeper investigation