A tour of mrcal: cross-validation
Previous
Overview
We now have a good method to evaluate the quality of a calibration: the projection uncertainty. Is that enough? If we run a calibration and see a low projection uncertainty, can we assume that the computed model is good, and use it moving forward? Once again, unfortunately, we cannot. A low projection uncertainty tells us that we're not sensitive to noise in the observed chessboard corners. However it says nothing about the effects of model errors.
Anything that makes our model not fit produces a model error. These can be caused by any of (for instance)
- out-of focus images
- images with motion blur
- rolling shutter effects
- camera synchronization errors
- chessboard detector failures
- insufficiently-rich models (of the lens or of the chessboard shape or anything else)
If model errors were present, then
- the computed projection uncertainty would underestimate the expected errors: the non-negligible model errors would be ignored
- the computed calibration would be biased: the residuals \(\vec x\) would be heteroscedastic, so the computed optimum would not be a maximum-likelihood estimate of the true calibration (see the noise modeling page)
By definition, model errors are unmodeled, so we cannot do anything with them analytically. Instead we try hard to force these errors to zero, so that we can ignore them. To do that, we need the ability to detect the presense of model errors. The solve diagnostics we talked about earlier are a good start. An even more powerful technique is computing a cross-validation diff:
- We gather not one, but two (or more) sets of chessboard observations
- We compute multiple independent calibrations of these cameras using these independent sets of observations
- We use the
mrcal-show-projection-difftool to compute the difference
The two separate calibrations sample the input noise and the model noise. This is, in effect, an empirical measure of uncertainty. If we gathered lots and lots of calibration datasets (many more than just two), the resulting empirical distribution of projections would conclusively tell us about the calibration quality. Usually we can quantify the response to input noise by computing just two empirical calibration samples and evaluating the projection uncertainty.
We want the model noise to be negligible; if it is, then the cross-validation diff contains sampling noise only, and the computed uncertainty becomes the authoritative gauge of calibration quality. In this case we would see a difference on the order of \(\mathrm{difference} \approx \mathrm{uncertainty}_0 + \mathrm{uncertainty}_1\). This is far from exact, and it would be good to define this more rigorously. But in practice, even this very loose definition is sufficient, and this technique works well. See below for more detail.
LENSMODEL_OPENCV8
For the Downtown LA dataset I did gather more than one set of images, so we can compute the cross-validation diff using this data. As a reminder, the computed dance-2 uncertainty (response to sampling error) looks like this:

The dance-3 uncertainty looks similar. The cross-validation diff looks like this:
mrcal-show-projection-diff \ --cbmax 2 \ --unset key \ 2-f22-infinity.opencv8.cameramodel \ 3-f22-infinity.opencv8.cameramodel
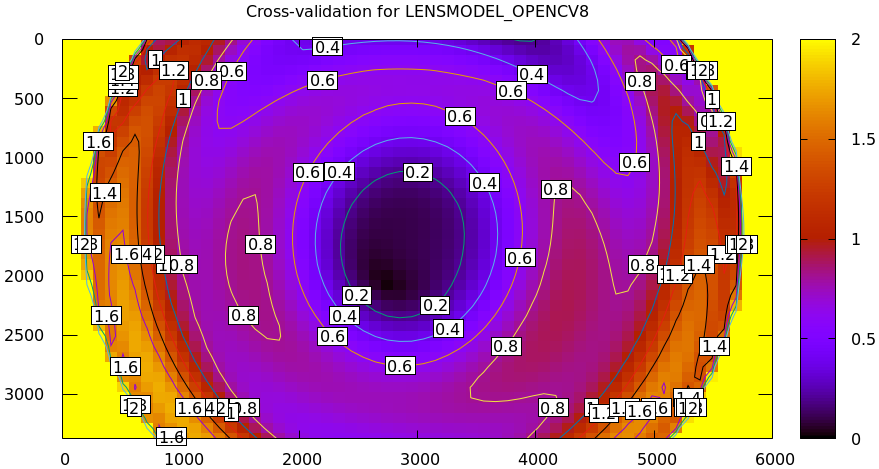
We already saw earlier evidence that LENSMODEL_OPENCV8 doesn't fit well, and
this confirms it. If we had low model errors, the cross-validation diff whould
be within ~0.2 pixels in most of the image. Clearly this model does far worse
than that, and we conclude that LENSMODEL_OPENCV8 doesn't fit well.
Comparing the uncertainty and the cross-validation
As noted above, we're looking for cross-validation on the order of \(\mathrm{difference} \approx \mathrm{uncertainty}_0 + \mathrm{uncertainty}_1\). This is crude for multiple reasons:
- Where in the imager are we looking?
- Where should the diff focus region be?
- How big should the focus region be?
And others. mrcal provides the analyses/validate-uncertainty.py tool to give
us a sense of how this behaves in practice. Given a solve, it adjusts the
observations to make the computed model fit exactly. Then it injects perfect
noise, resolves and computes a diff. This is precisely what computing the
cross-validation does in the case where the model error is zero. Let's run it on
this LENSMODEL_OPENCV8 solve:
analyses/validate-uncertainty.py \ --cbmax-uncertainty 1 \ --cbmax-diff 2 \ --num-samples 25 \ 2-f22-infinity.opencv8.cameramodel
We get a whole lot of cross-validation samples:

And we can average them:
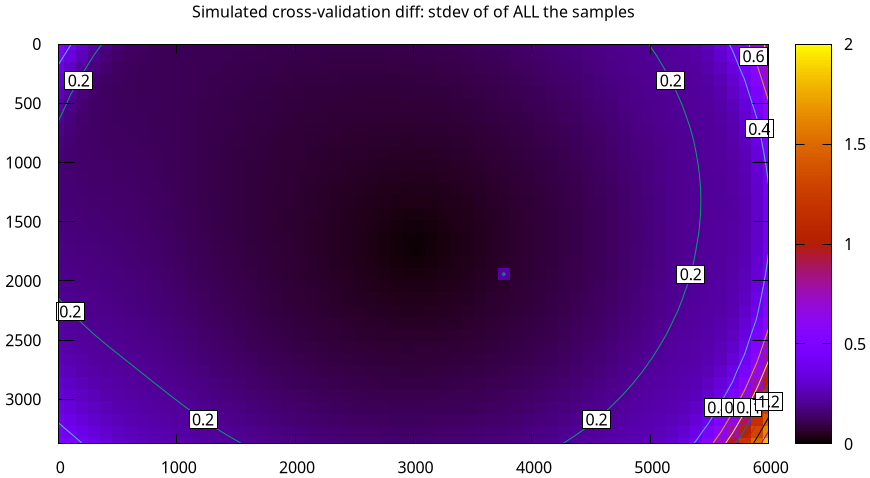
This is about double the uncertainty, as claimed. So if we see a cross-validation sample that's far above double the uncertainty, either we got really unlucky or we have model errors.
LENSMODEL_SPLINED_STEREOGRAPHIC
Back to evaluating the models. We just got confirmation that LENSMODEL_OPENCV8
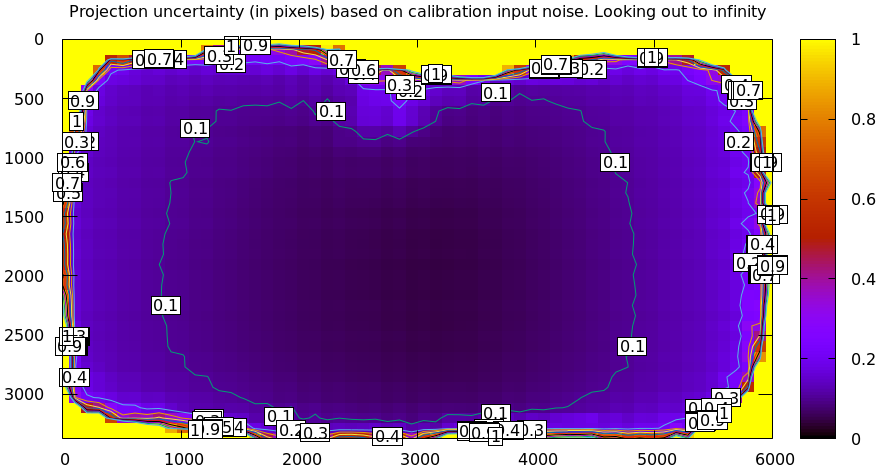
doesn't fit well. We expect the splined model to do better. The dance-2
uncertainty from before:
And the cross-validation diff:
mrcal-show-projection-diff \ --cbmax 2 \ --unset key \ 2-f22-infinity.splined.cameramodel \ 3-f22-infinity.splined.cameramodel
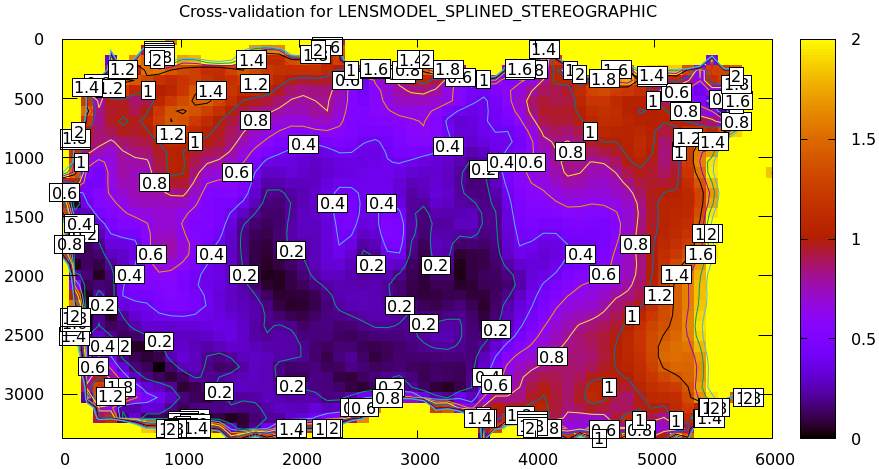
Much better. It's a big improvement LENSMODEL_OPENCV8, but it's still
noticeably not fitting. So we can explain ~0.2-0.4 pixels of the error away from
the edges (twice the uncertainty), but the rest is unexplained. Thus any
application that requires an accuracy of <1 pixel would have problems with this
calibration.
For completeness, the simulated mean cross-validation diff for this model:
analyses/validate-uncertainty.py \ --cbmax-uncertainty 1 \ --cbmax-diff 2 \ --num-samples 25 \ 2-f22-infinity.splined.cameramodel

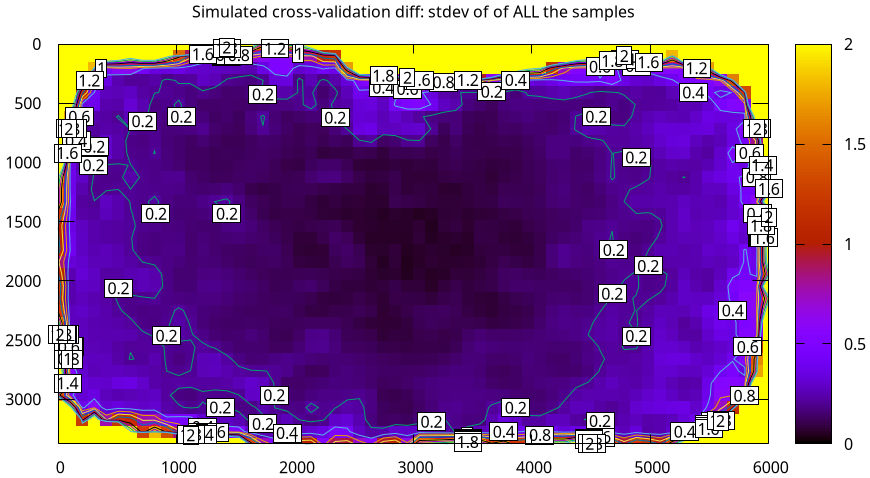
Once again we see the average diff being ~ 2x the uncertainty. This is a empirical mean of not a huge number of samples, so it's crude, but supports the overall idea: seeing a cross-validations higher-than-2x-uncertainty should warrant a deeper look.
Improving it further
I know from past experience with this lens that the biggest problem here is caused by mrcal assuming a central projection in its models: it assumes that all rays intersect at a single point. This is an assumption made by more or less every calibration tool, and most of the time it's reasonable. However, this assumption breaks down when you have a physically large, wide-angle lens looking at objects very close to the lens: exactly the case we have here.
In most cases, you will never use the camera system to observe extreme closeups, so it is reasonable to assume that the projection is central. But this assumption breaks down if you gather calibration images so close as to need the noncentral behavior. If the calibration images were gathered from too close, we would see a too-high cross-validation diff, as we have here. The recommended remedy is to gather new calibration data from further out, to minimize the noncentral effects. The current calibration images were gathered from very close-in to maximize the projection uncertainty. So getting images from further out would produce a higher-uncertainty calibration, and we would need to capture a larger number of chessboard observations to compensate.
Here I did not gather new calibration data, so we do the only thing we can: we model the noncentral behavior. A branch of mrcal contains an experimental and not-entirely-complete support for noncentral projections. I solved this calibration problem with that code, and the result does fit our data much better. The cross-validation diff:
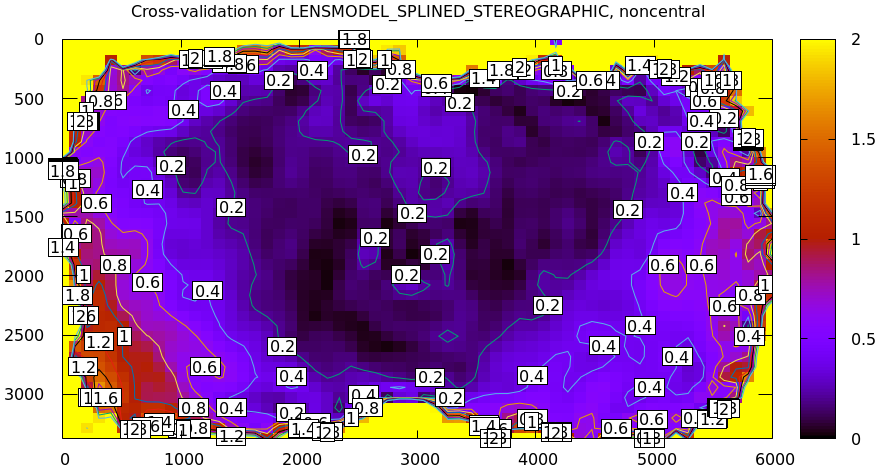
This still isn't perfect, but it's close. The noncentral projection support is not yet done. Talk to me if you need it.
A more rigorous interpretation of these cross-validation results would be good, but a human interpretation is working well, so it's low-priority for me at the moment.