Triangulation methods and uncertainty
Table of Contents
\( \DeclareMathOperator*{\argmin}{argmin} \DeclareMathOperator*{\Var}{Var} \)
A very common thing to want to do with a calibrated camera system is to convert a pair of pixel observations of a feature to a point in space that produced these observations, a process known as triangulation. mrcal supports both sparse triangulation (processing a small number of discrete pixel observations) and dense triangulation (processing every pixel in a pair of images; stereo vision). This can be sensitive to noise, creating a strong need for proper error modeling and propagation.
Here I describe mrcal's sparse triangulation capabilities: the
mrcal-triangulate tool and the mrcal.triangulate() Python routine.
Overview
Let's say we have an idealized geometry:
Let \(b \equiv \mathrm{baseline}\) and \(r \equiv \mathrm{range}\). Two cameras are looking at a point in space. Given two camera models and a pair of pixel observations we can compute the range to the point. Basic geometry tells us that
\[\frac{r}{\sin \phi} = \frac{b}{\sin \theta}\]
When looking far away, straight ahead, we have \(\theta \approx 0\) and \(\phi \approx 90^\circ\), so
\[ r \approx \frac{b}{\theta}\]
Differentiating, we get
\[\frac{\mathrm{d}r}{\mathrm{d}\theta} \propto \frac{b}{\theta^2} \propto \frac{r^2}{b}\]
Thus a small error in \(\theta\) causes an error in the computed range that is proportional to the square of \(r\). This relationship sets the fundamental limit for the ranging capabilities of stereo systems: if you try to look out too far, the precision of \(\theta\) required to get a precise-enough \(r\) becomes unattainable. And because we have \(r^2\), this range limit is approached very quickly. A bigger baseline helps, but does so only linearly.
The angle \(\theta\) comes from the extrinsics and intrinsics in the camera model, so the noise modeling and uncertainty propagation in mrcal are essential to a usable long-range stereo system.
Triangulation routines
Before we can talk about quantifying the uncertainty of a triangulation operation, we should define what that operation is. Each triangulation operation takes as input
- Two camera models. Intrinsics (lens behavior) and extrinsics (geometry) are required for both
- Pixel coordinates \(\vec q\) of the same observed feature in the two images captured by each camera
And it outputs
- A point \(\vec p\) in space that produced the given pixel observations
The "right" way to implement this operation is to minimize the reprojection error:
\[ E\left(\vec p\right) \equiv \left\lVert \vec q_0 - \mathrm{project}_\mathrm{cam0}\left(\vec p\right) \right\rVert^2 + \left\lVert \vec q_1 - \mathrm{project}_\mathrm{cam1}\left(\vec p\right) \right\rVert^2 \]
\[ \vec p^* \equiv \argmin{E\left(\vec p\right)} \]
This is correct, but it's complex and requires a nonlinear optimization, which limits the usefulness of this approach. mrcal implements several slightly-imprecise but much faster methods to compute a triangulation. All of these precompute \(\vec v \equiv \mathrm{unproject} \left( \vec q \right)\), and then operate purely geometrically. The methods are described in these papers, listed in chronological order:
- "Triangulation Made Easy", Peter Lindstrom. IEEE Conference on Computer Vision and Pattern Recognition, 2010
- "Closed-Form Optimal Two-View Triangulation Based on Angular Errors", Seong Hun Lee and Javier Civera. https://arxiv.org/abs/1903.09115
- "Triangulation: Why Optimize?", Seong Hun Lee and Javier Civera https://arxiv.org/abs/1907.11917
The last paper compares the available methods from all the papers. A
triangulation study is available to evaluate the precision and accuracy of the
existing methods. Currently leecivera_mid2 is recommended for most usages.
Note that all of the Lee-Civera methods work geometrically off observation vectors, not pixel coordinates directly. This carries an implicit assumption that the angular resolution is constant across the whole imager. This is usually somewhat true, but the extent depends on the specific lens and camera. Use the resolution-visualization tool to check.
The triangulation methods available in mrcal:
geometric
This is the basic midpoint method: it computes the point in space that minimizes
the distance between the two observation rays. This is the simplest method, but
also produces the most bias. Not recommended. Implemented in
mrcal.triangulate_geometric() (in Python) and mrcal_triangulate_geometric()
(in C).
lindstrom
Described in the "Triangulation Made Easy" paper above. The method is a close
approximation to a reprojection error minimization (the "right" approach above)
if we have pinhole lenses. Implemented in mrcal.triangulate_lindstrom() (in
Python) and mrcal_triangulate_lindstrom() (in C).
leecivera_l1
Described in the "Closed-Form Optimal Two-View Triangulation Based on Angular
Errors" paper above. Minimizes the L1 norm of the observation angle error.
Implemented in mrcal.triangulate_leecivera_l1() (in Python) and
mrcal_triangulate_leecivera_l1() (in C).
leecivera_linf
Described in the "Closed-Form Optimal Two-View Triangulation Based on Angular
Errors" paper above. Minimizes the L-infinity norm of the observation angle
error. Implemented in mrcal.triangulate_leecivera_linf() (in Python) and
mrcal_triangulate_leecivera_linf() (in C).
leecivera_mid2
Described in the "Triangulation: Why Optimize?" paper above: this is the "Mid2"
method. Doesn't explicitly minimize anything, but rather is a heuristic that
works well in practice. Implemented in mrcal.triangulate_leecivera_mid2() (in
Python) and mrcal_triangulate_leecivera_mid2() (in C).
leecivera_wmid2
Described in the "Triangulation: Why Optimize?" paper above: this is the "wMid2"
method. Doesn't explicitly minimize anything, but rather is a heuristic that
works well in practice. Similar to leecivera_mid2, but contains a bit of extra
logic to improve the behavior for points very close to the cameras (not
satisfying \(r \gg b\)). Implemented in mrcal.triangulate_leecivera_wmid2() (in
Python) and mrcal_triangulate_leecivera_wmid2() (in C).
Triangulation uncertainty
We compute the uncertainty of a triangulation operation using the usual error-propagation technique:
- We define the input noise
- We compute the operation through which we're propagating this input noise, evaluating the gradients of the output in respect to all the noisy inputs
- We assume the behavior is locally linear and that the input noise is Gaussian, which allows us to easily compute the output noise using the usual noise-propagation relationship
Noise sources
We want to capture the effect of two different sources of error:
- Calibration-time noise. We propagate the noise in chessboard observations
obtained during the chessboard dance. This is the noise that we propagate when
evaluating projection uncertainty. This is specified in the
--q-calibration-stdevargument tomrcal-triangulateor in theq_calibration_stdevargument tomrcal.triangulate(). This is usually known from the calibration, and we can request the calibrated value by passing a stdev of -1. See the relevant interface documentation (just-mentioned links) for details. Observation-time noise. Each triangulation processes observations \(\vec q\) of a feature in space. These are noisy, and we propagate that noise. As with calibration-time noise, this noise is assumed to be normally distributed and independent in \(x\) and \(y\). This is specified in the
--q-observation-stdevargument tomrcal-triangulateor in theq_observation_stdevargument tomrcal.triangulate(). A common source of these pixel observations is a pixel correlation operation where a patch in one image is matched against the second image. Corresponding pixel observations observed this way are correlated: the noise in \(\vec q_0\) not independent of the noise in \(\vec q_1\). I do not yet know how to estimate this correlation, but the tools are able to ingest and propagate such an estimate: using the--q-observation-stdev-correlationcommandline option tomrcal-triangulateor theq_observation_stdev_correlationargument tomrcal.triangulate().Note that when thinking about observation-time noise in dense stereo processing, we generally assume that \(\vec q_0\) is known perfectly and that there is no correlation at all between the \(\vec q_0\) and \(\vec q_1\) observations. A bit more thought is needed to figure out how to talk about this noise propagation properly.
A big point to note here is that repeated observations of the same feature have independent observation-time noise. So these observation-time errors average out with multiple observations. This is not true of the calibration-time noise however. Using the same calibration to observe a feature multiple times will produce correlated triangulation results. So calibration-time noise is biased, and it is thus essential to make and use low-uncertainty calibrations to minimize this effect.
Example uncertainties
The test-triangulation-uncertainty.py test generates synthetic models and
triangulation scenarios. It can be used to produce an illustrative diagram:
test/test-triangulation-uncertainty.py \ --do-sample \ --cache write \ --observed-point -2 0 10 \ --fixed cam0 \ --Nsamples 200 \ --Ncameras 2 \ --q-observation-stdev-correlation 0.5 \ --q-calibration-stdev 0.2 \ --q-observation-stdev 0.2 \ --make-documentation-plots ''
Here we have two cameras arranged in the usual left/right stereo configuration, looking at two points at (-2,10)m and (2,10)m. We generate calibration and observation noise, and display the results in the horizontal plane. The vertical dimension is insignificant here, so it is not shown, even though all the computations are performed in full 3D. For each of the two observed points we display:
- The empirical noise samples, and the 1-sigma ellipse they represent
- The predicted 1-sigma ellipse for the calibration-time noise
- The predicted 1-sigma ellipse for the observation-time noise
- The predicted 1-sigma ellipse for the joint noise
We can see that the observed and predicted covariances line up nicely. We can also see that the observation-time noise acts primarily in the forward/backward direction, while the calibration-time noise has a much larger lateral effect. This pattern varies greatly depending on the lenses and the calibration and the geometry. As we get further out, the uncertainty in the forward/backward direction dominates for both noise sources, as expected.
Stabilization
In the above plot, the uncertainties are displayed in the coordinate system of the left camera. But, as described on the projection uncertainty page, the origin and orientation of each camera's coordinate system is subject to calibration noise:
So what we usually want to do is to consider the covariance of the triangulation in the coordinates of the camera housing, not the camera coordinate system. We achieve this with "stabilization", computed exactly as described on the projection uncertainty page. We can recompute the triangulation uncertainty in the previous example (same geometry, lens, etc), but with stabilization enabled:
test/test-triangulation-uncertainty.py \ --do-sample \ --cache write \ --observed-point -2 0 10 \ --fixed cam0 \ --Nsamples 200 \ --Ncameras 2 \ --q-observation-stdev-correlation 0.5 \ --q-calibration-stdev 0.2 \ --q-observation-stdev 0.2 \ --stabilize \ --make-documentation-plots ''
We can now clearly see that the forward/backward uncertainty was a real effect, but the lateral uncertainty was largely due to the moving camera coordinate system.
Calibration-time noise produces correlated estimates
As mentioned above, the calibration-time noise produces correlations (and thus
biases) in the triangulated measurements. Since the
test-triangulation-uncertainty.py command triangulates two different points,
we can directly observe these correlations. Let's look at the magnitude of each
element of \(\Var {\vec p_{01}}\) where \(\vec p_{01}\) is a 6-dimensional vector
that contains both the triangulated 3D points: \(\vec p_{01} \equiv
\left[ \begin{array}{cc} \vec p_0 \\ \vec p_1 \end{array} \right]\). If we had
only observation-time noise, \(\vec p_0\) and \(\vec p_1\) would be independent,
and the off-diagonal terms in the covariance matrix would be 0. However, we also
have calibration-time noise, so the errors are correlated:
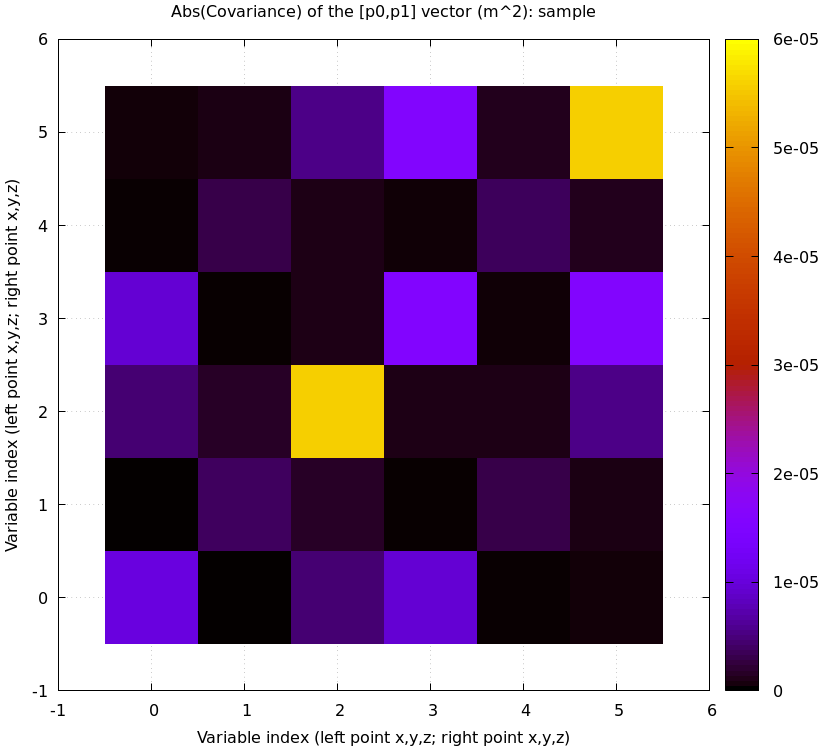
As before, the exact pattern varies greatly depending on the lenses and the calibration and the geometry, but calibration-time noise always creates these correlations. To reduce these correlations and the biases they cause: lower the uncertainty of your calibrations by dancing better
Assumptions break down at infinity
When propagating noise, mrcal makes the very common assumption that everything is locally linear. This makes things simple, and is right most of the time. However, when running the triangulation routines with near-parallel rays, this assumptions can break down.
Let's run another simulation, but observing a more distant point, with more observation-time noise, no calibration-time noise, and gathering more samples:
test/test-triangulation-uncertainty.py \ --do-sample \ --cache write \ --observed-point -200 0 2000 \ --fixed cam0 \ --Nsamples 2000 \ --Ncameras 2 \ --q-observation-stdev-correlation 0.5 \ --q-observation-stdev 0.4 \ --stabilize \ --make-documentation-plots ''
The range to the observed point:
The two points in the synthetic world are at \((\pm 200, 0, 2000)m\) so the true range is ~ \(2010m\). We see that the calibration-time noise has little effect here. More importantly, we also see that the predicted distribution of the range to the point is gaussian (as we assume), but the empirical distribution is not gaussian: there's a much more significant tail on the long end. This makes sense. If the observation rays are near-parallel, small errors that make the rays more parallel push the range to infinity; while small errors that bring the rays together have a more modest, finite effect.
Similarly, when we look at the distance between our two points we get this distribution:
We see the same asymmetric non-gaussian distribution. Empirically I observe this distance-between-points distribution become more non-gaussian, faster than the range-to-point distribution.
At this time I do not know how much this matters or what to do about it, but these limitations are good to keep in mind.
Applications
Visual tracking of an object over time is one application that would benefit
from a more complete error model of its input. Repeated noisy observations of a
moving object \(\vec q_{01}(t)\) can be triangulated into a noisy estimate of the
object motion \(\vec p(t)\). If for each point in time \(t\) we have \(\Var \vec
p(t)\), we can combine everything into an estimate \(\hat p(t)\). The better our
covariances, the closer the estimate. The mrcal.triangulate() routine can be
used to compute the triangulations, and to report the full covariances matrices.
Applying these techniques
See the tour of mrcal for an application of these routines to real-world data