A tour of mrcal: range dependence
The effect of range in differencing and uncertainty computations
Earlier I talked about model differencing and estimation of projection uncertainty. In both cases I glossed over one important detail that I would like to revisit now. A refresher:
- To compute a diff, I unproject \(\vec q_0\) to a point in space \(\vec p\) (in camera coordinates), transform it, and project that back to the other camera to get \(\vec q_1\)
- To compute an uncertainty, I unproject \(\vec q_0\) to (eventually) a point in space \(\vec p_\mathrm{fixed}\) (in some fixed coordinate system), then project it back, propagating all the uncertainties of all the quantities used to compute the transformations and projection.
The significant part is the specifics of "unproject \(\vec q_0\)". Unlike a projection operation, an unprojection is ambiguous: given some camera-coordinate-system point \(\vec p\) that projects to a pixel \(\vec q\), we have \(\vec q = \mathrm{project}\left(k \vec v\right)\) for all \(k\). So an unprojection gives you a direction, but no range. What that means in this case, is that we must choose a range of interest when computing diffs or uncertainties. It only makes sense to talk about a "diff when looking at points \(r\) meters away" or "the projection uncertainty when looking out to \(r\) meters".
A surprising consequence of this is that while projection is invariant to scaling (\(k \vec v\) projects to the same \(\vec q\) for all \(k\)), the uncertainty of this projection is not:
Let's look at the projection uncertainty at the center of the imager at
different ranges for the LENSMODEL_OPENCV8 model we computed earlier:
mrcal-show-projection-uncertainty \ --vs-distance-at center \ --set 'yrange [0:0.1]' \ opencv8.cameramodel
So the uncertainty grows without bound as we approach the camera. As we move away, there's a sweet spot where we have maximum confidence. And as we move further out still, we approach some uncertainty asymptote at infinity. Qualitatively this is the figure I see 100% of the time, with the position of the minimum and of the asymptote varying.
Why is the uncertainty unbounded as we approach the camera? Because we're looking at the projection of a fixed point into a camera whose position is uncertain. As we get closer to the origin of the camera, the noise in the camera position dominates the projection, and the uncertainty shoots to infinity.
What controls the range where we see the lowest uncertainty? The range where we observed the chessboards. I will prove this conclusively in the next section. It makes sense: the best uncertainty corresponds to the region where we have the most information.
What controls the uncertainty at infinity? The empirical studies in the next section answer that conclusively.
This is a very important effect to characterize. In many applications the distance of observations at calibration time varies significantly from the working distance post-calibration. For instance, any application involving wide lenses will use closeup calibration images, but working images from much further out. We don't want to compute a calibration where the calibration-range uncertainty is great, but the working-range uncertainty is poor.
I should emphasize that while unintuitive, this uncertainty-depends-on-range effect is very real. It isn't just something that you get out of some opaque equations, but it's observable in the field. We can't see it in the cross validation diffs we just computed because the noncentral model errors dominate, but if we throw out all the observations away from the center, the noncentral errors disappear, and the effect is clearly seen empirically.
I threw out all points outside of a circle in the center with radius 1500 pixels
(using the mrcal-cull-corners tool). Cross-validation diff at 1m (chessboards
are here; we expect this to be low):

And at infinity (uncertainty plot tells us that this should be ~ 3x worse):
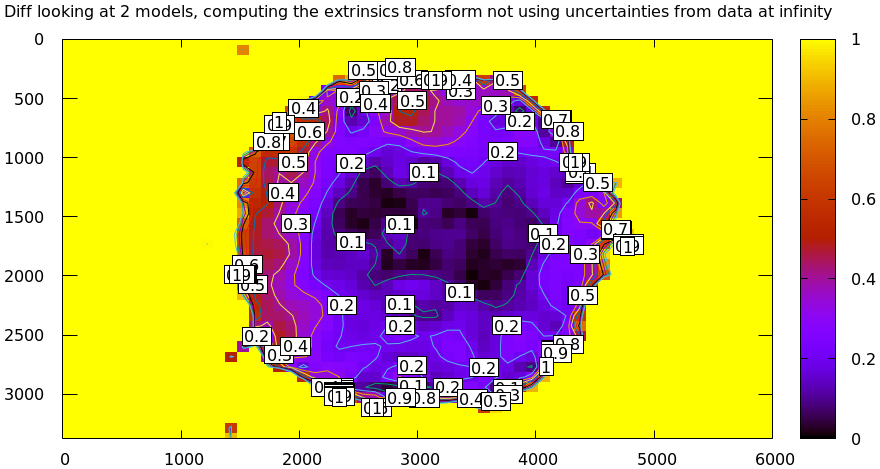
Clearly the prediction that uncertainties are lowest at the chessboard distance, and increase as we move away is borne out here empirically, by just looking at diffs. Without computing the uncertainty curves. This effect is universal, and is especially clear when the uncertainties at the chessboard distance and at infinity are very different. How do we make sure that the uncertainty at infinity is still low, despite the fact that no chessboards were observed there? Read on.
Next
We're now ready to find the best chessboard-dancing technique.